● भुज (abscissa) - किसी बिंदु की y-अक्ष से दुरी को x-निर्देशांक अथवा भुज कहते हैं।
● कोटि (ordinate) - किसी बिंदु की x-अक्ष से दुरी को y-निर्देशांक अथवा कोटि कहते हैं।
● किसी बिंदु के भुज और कोटि (x, y) के रूप में होते हैं।
● दो बिंदुओं A(x1, y1) और B(x2, y2) के बीच की दुरी इस सूत्र के हल के बराबर होती है -

● किसी बिंदु A(x, y) की मूलबिन्दु से दूरी इस सूत्र के हल के बराबर होती है -

● बिंदुओं A(x1, y1) और B(x2, y2) को जोड़ने वाले रेखाखंड (line segment) को m1:m2 के अनुपात में आंतरिक रूप से विभाजित करने वाले उस बिंदु L(x, y) के निर्देशांक (coordinates) ये होते हैं -

इसे विभाजन सूत्र (split formula) कहते हैं।
● यदि कोई P रेखाखंड AB को k:1 में विभाजित करता है, तो बिंदु P के निर्देशांक निम्नलिखित होते हैं -

● दो बिंदुओं A(x1, y1) और B(x2, y2) को मिलाने वाले रेखाखंड के मध्यबिंदु (mid-point) के निर्देशांक ये होते हैं -
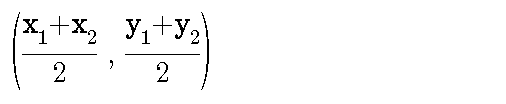
● कार्तीय तल (cartesian plane) पर स्थित तीन बिंदुओं A(x1, y1), B(x2, y2) और C(x3, y3) से बने त्रिभुज का क्षेत्रफल के लिए सूत्र -

● आपको कार्तीय तल पर स्थित कुछ बिंदु दिए गए हैं तो पहले उन्हें अंकित करो और फिर आगे हल करो।
● दिए गए बिंदुओं के बीच यदि कोई सम्बन्ध (relation) पाया जाता है, तो उस सम्बन्ध के आधार पर बिना कार्तीय तल के भी उत्तर प्राप्त करना सम्भव (possible) है।
● यदि कोई बिंदु P(x, y) दो अन्य बिंदुओं
Q(x1, y1) और R(x2, y2) से समदूरस्थ (समान दुरी पर/ equidistant) हो, तो उस बिंदु के निर्देशांक निम्न का हल होता है -
● कोटि (ordinate) - किसी बिंदु की x-अक्ष से दुरी को y-निर्देशांक अथवा कोटि कहते हैं।
● किसी बिंदु के भुज और कोटि (x, y) के रूप में होते हैं।
● दो बिंदुओं A(x1, y1) और B(x2, y2) के बीच की दुरी इस सूत्र के हल के बराबर होती है -

● किसी बिंदु A(x, y) की मूलबिन्दु से दूरी इस सूत्र के हल के बराबर होती है -

● बिंदुओं A(x1, y1) और B(x2, y2) को जोड़ने वाले रेखाखंड (line segment) को m1:m2 के अनुपात में आंतरिक रूप से विभाजित करने वाले उस बिंदु L(x, y) के निर्देशांक (coordinates) ये होते हैं -

इसे विभाजन सूत्र (split formula) कहते हैं।
● यदि कोई P रेखाखंड AB को k:1 में विभाजित करता है, तो बिंदु P के निर्देशांक निम्नलिखित होते हैं -

● दो बिंदुओं A(x1, y1) और B(x2, y2) को मिलाने वाले रेखाखंड के मध्यबिंदु (mid-point) के निर्देशांक ये होते हैं -
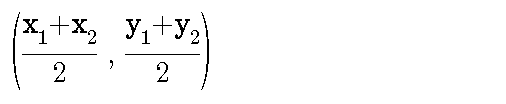
● कार्तीय तल (cartesian plane) पर स्थित तीन बिंदुओं A(x1, y1), B(x2, y2) और C(x3, y3) से बने त्रिभुज का क्षेत्रफल के लिए सूत्र -

● आपको कार्तीय तल पर स्थित कुछ बिंदु दिए गए हैं तो पहले उन्हें अंकित करो और फिर आगे हल करो।
● दिए गए बिंदुओं के बीच यदि कोई सम्बन्ध (relation) पाया जाता है, तो उस सम्बन्ध के आधार पर बिना कार्तीय तल के भी उत्तर प्राप्त करना सम्भव (possible) है।
● यदि कोई बिंदु P(x, y) दो अन्य बिंदुओं
Q(x1, y1) और R(x2, y2) से समदूरस्थ (समान दुरी पर/ equidistant) हो, तो उस बिंदु के निर्देशांक निम्न का हल होता है -

All Mathematics Chapters Notes for 10th standard :-
अध्याय - 1 वास्तविक संख्याए
अध्याय 2 बहुपद
अध्याय 3 दो चरों वाले रैखिक समीकरण युग्म
अध्याय 4 द्विघात समीकरण
अध्याय 5 समांतर श्रेढ़ी
अध्याय 6 त्रिभुज
अध्याय 7 निर्देशांक ज्यामिति
अध्याय 8 त्रिकोणमिति का परिचय
अध्याय 9 त्रिकोणमिति के कुछ अनुप्रयोग
अध्याय 10 वृत्त
अध्याय 11 रचनाएँ
अध्याय 12 वृत्तों से संबंधित क्षेत्रफल
अध्याय 13 पृष्ठीय क्षेत्रफल और आयतन
अध्याय 14 सांख्यिकी
अध्याय 15 प्रायिकता
अध्याय 2 बहुपद
अध्याय 3 दो चरों वाले रैखिक समीकरण युग्म
अध्याय 4 द्विघात समीकरण
अध्याय 5 समांतर श्रेढ़ी
अध्याय 6 त्रिभुज
अध्याय 7 निर्देशांक ज्यामिति
अध्याय 8 त्रिकोणमिति का परिचय
अध्याय 9 त्रिकोणमिति के कुछ अनुप्रयोग
अध्याय 10 वृत्त
अध्याय 11 रचनाएँ
अध्याय 12 वृत्तों से संबंधित क्षेत्रफल
अध्याय 13 पृष्ठीय क्षेत्रफल और आयतन
अध्याय 14 सांख्यिकी
अध्याय 15 प्रायिकता


![सांख्यिकी {Statistics} [Chapter 14, Class IX]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi_Eie0g-2Q4WFhuq33fcbGc6APTAUgrqjls1icjZOeRuojnetcOlKLR-xFI9kWja-9vZYS968WIH5_w0nlOXC0SN8JiNSQfShnqHpcRjoLAOJ9QcIc48SIXNzPEhiCYgJJGs5dz_smlY0j/s72-c/Statistics+Class+9+CBSE.jpg)

कोई टिप्पणी नहीं
Thanks for your comments !