● दो चरों में रैखिक समीकरण (linear pair in two variables) - जिस समीकरण को
ax + by + c = 0 के रूप में रखा जा सके, जहाँ a, b और c वास्तविक संख्याएँ हैं, तथा a और b दोनों शून्य नहीं हो सकते, x और y में रैखिक समीकरण कहलाता है।
● किसी भी दो चरों वाले रैखिक समीकरण
(ax + by + c = 0) का प्रत्येक हल (x, y) इस समीकरण को निरूपित करने वाली रेखा पर स्थित एक बिंदु होता है। इसका विलोमशः (opposite) भी सत्य है।
● दो चरों वाले रैखिक समीकरण का ज्यामितीय निरूपण (graph) एक सरल अर्थात सीधी रेखा होती है।
● एक तल में दो रेखाएँ दी होने पर निम्न में से कोई एक सम्भावना हो सकती है -
* समान्तर रेखाएँ (parallel lines)
* प्रतिच्छेदी रेखाएँ (interesting lines)
* संपाती रेखाएँ (coincident lines)
● दो चरों वाले रैखिक समीकरण युग्म (pair) के हल ग्राफ पर दो सरल रेखाएँ होती हैं, जिनमें उपरोक्त में से कोई एक सम्बन्ध हो सकता है।
* रेखाएँ समान्तर हुई तो दो चरों में रैखिक समीकरण का कोई हल नहीं (no solution) होगा। इस प्रकार के रैखिक समीकरण युग्म को असंगत युग्म (inconsistent pair) कहा जाता है।
* रेखाएँ प्रतिच्छेदी हुई तो दो चरों में रैखिक समीकरण का केवल एक अद्वितीय हल (unique solution) होगा। इस प्रकार के रैखिक समीकरण युग्म संगत युग्म (consistent pair) कहलाते हैं।
* रेखाएँ संपाती हुई तो दो चरों में रैखिक समीकरण के असीमित हल (infinitely many solutions) होंगे। इस प्रकार के रैखिक समीकरण को आश्रित युग्म (dependent pair) कहा जाता है और आश्रित युग्म हमेशा संगत होता है।
● दो रैखिक समीकरण युग्म इस रूप के होते हैं -

* रेखाएँ प्रतिच्छेद करें तो a1/a2 बराबर नहीं होगा b1/b2
* रेखाएँ समान्तर हुई तो a1/a2 = b1/b2 लेकिन c1/c2 बराबर नहीं होगा।
* रेखाएँ संपाती हुई तो a1/a2 = b1/b2 = c1/c2
● रैखिक समीकरण युग्म को हल करने की विधियाँ -
➡ प्रतिस्थापन विधि (substitution method) - रैखिक समीकरण युग्म में से किसी भी समीकरण को x या y के मान में ज्ञात करके दूसरे समीकरण में प्रतिस्थापित करके मान ज्ञात करने की विधि को प्रतिस्थापन विधि कहते हैं।
➡ विलोपन विधि (elimination method) - रैखिक समीकरण युग्म में पहले समीकरण के x या y के गुणांक से दूसरे समीकरण में तथा दूसरे समीकरण के उसी चर के गुणांक से पहले समीकरण में गुणा (multiply) करो और फिर बड़े मान वाले समीकरण में से छोटे मान वाले समीकरण को घटाकर मान ज्ञात करने की विधि को विलोपन विधि कहा जाता है।
नोट: इस विधि में या तो x के गुणांक को बराबर किया जाता है या y के गुणांक को बराबर किया जाता है।
➡ वज्र-गुणन विधि (cross multiplication method)
● रैखिक समीकरण युग्म
के मानों को निम्न रूप में लिखते हैं
और x और y के मान ज्ञात करते हैं, जहाँ
a1b2 - a2b1 बराबर नहीं शून्य के।
● जो समीकरण ax + by + c = 0 के रूप के न हो उन्हें पहले a और b के उभयनिष्ठ गुणनखंड (common factor) के स्थान पर कोई अन्य अक्षर मानकर इस रूप में परिवर्तित किया जाता है और फिर हल किया जाता है।
● किसी भी रैखिक समीकरण युग्म का ग्राफीय प्रदर्शन (graphic representation) कर सकते हैं और इसे ग्राफ विधि और बीजगणितीय विधि (algebric method) द्वारा हल कर सकते हैं।
ax + by + c = 0 के रूप में रखा जा सके, जहाँ a, b और c वास्तविक संख्याएँ हैं, तथा a और b दोनों शून्य नहीं हो सकते, x और y में रैखिक समीकरण कहलाता है।
● किसी भी दो चरों वाले रैखिक समीकरण
(ax + by + c = 0) का प्रत्येक हल (x, y) इस समीकरण को निरूपित करने वाली रेखा पर स्थित एक बिंदु होता है। इसका विलोमशः (opposite) भी सत्य है।
● दो चरों वाले रैखिक समीकरण का ज्यामितीय निरूपण (graph) एक सरल अर्थात सीधी रेखा होती है।
● एक तल में दो रेखाएँ दी होने पर निम्न में से कोई एक सम्भावना हो सकती है -
* समान्तर रेखाएँ (parallel lines)
* प्रतिच्छेदी रेखाएँ (interesting lines)
* संपाती रेखाएँ (coincident lines)
● दो चरों वाले रैखिक समीकरण युग्म (pair) के हल ग्राफ पर दो सरल रेखाएँ होती हैं, जिनमें उपरोक्त में से कोई एक सम्बन्ध हो सकता है।
* रेखाएँ समान्तर हुई तो दो चरों में रैखिक समीकरण का कोई हल नहीं (no solution) होगा। इस प्रकार के रैखिक समीकरण युग्म को असंगत युग्म (inconsistent pair) कहा जाता है।
* रेखाएँ प्रतिच्छेदी हुई तो दो चरों में रैखिक समीकरण का केवल एक अद्वितीय हल (unique solution) होगा। इस प्रकार के रैखिक समीकरण युग्म संगत युग्म (consistent pair) कहलाते हैं।
* रेखाएँ संपाती हुई तो दो चरों में रैखिक समीकरण के असीमित हल (infinitely many solutions) होंगे। इस प्रकार के रैखिक समीकरण को आश्रित युग्म (dependent pair) कहा जाता है और आश्रित युग्म हमेशा संगत होता है।
● दो रैखिक समीकरण युग्म इस रूप के होते हैं -
* रेखाएँ प्रतिच्छेद करें तो a1/a2 बराबर नहीं होगा b1/b2
* रेखाएँ समान्तर हुई तो a1/a2 = b1/b2 लेकिन c1/c2 बराबर नहीं होगा।
* रेखाएँ संपाती हुई तो a1/a2 = b1/b2 = c1/c2
● रैखिक समीकरण युग्म को हल करने की विधियाँ -
➡ प्रतिस्थापन विधि (substitution method) - रैखिक समीकरण युग्म में से किसी भी समीकरण को x या y के मान में ज्ञात करके दूसरे समीकरण में प्रतिस्थापित करके मान ज्ञात करने की विधि को प्रतिस्थापन विधि कहते हैं।
➡ विलोपन विधि (elimination method) - रैखिक समीकरण युग्म में पहले समीकरण के x या y के गुणांक से दूसरे समीकरण में तथा दूसरे समीकरण के उसी चर के गुणांक से पहले समीकरण में गुणा (multiply) करो और फिर बड़े मान वाले समीकरण में से छोटे मान वाले समीकरण को घटाकर मान ज्ञात करने की विधि को विलोपन विधि कहा जाता है।
नोट: इस विधि में या तो x के गुणांक को बराबर किया जाता है या y के गुणांक को बराबर किया जाता है।
➡ वज्र-गुणन विधि (cross multiplication method)
● रैखिक समीकरण युग्म
के मानों को निम्न रूप में लिखते हैं
और x और y के मान ज्ञात करते हैं, जहाँ
a1b2 - a2b1 बराबर नहीं शून्य के।
● जो समीकरण ax + by + c = 0 के रूप के न हो उन्हें पहले a और b के उभयनिष्ठ गुणनखंड (common factor) के स्थान पर कोई अन्य अक्षर मानकर इस रूप में परिवर्तित किया जाता है और फिर हल किया जाता है।
● किसी भी रैखिक समीकरण युग्म का ग्राफीय प्रदर्शन (graphic representation) कर सकते हैं और इसे ग्राफ विधि और बीजगणितीय विधि (algebric method) द्वारा हल कर सकते हैं।
All Mathematics Chapters Notes for 10th standard :-
अध्याय - 1 वास्तविक संख्याए
अध्याय 2 बहुपद
अध्याय 3 दो चरों वाले रैखिक समीकरण युग्म
अध्याय 4 द्विघात समीकरण
अध्याय 5 समांतर श्रेढ़ी
अध्याय 6 त्रिभुज
अध्याय 7 निर्देशांक ज्यामिति
अध्याय 8 त्रिकोणमिति का परिचय
अध्याय 9 त्रिकोणमिति के कुछ अनुप्रयोग
अध्याय 10 वृत्त
अध्याय 11 रचनाएँ
अध्याय 12 वृत्तों से संबंधित क्षेत्रफल
अध्याय 13 पृष्ठीय क्षेत्रफल और आयतन
अध्याय 14 सांख्यिकी
अध्याय 15 प्रायिकता
अध्याय 2 बहुपद
अध्याय 3 दो चरों वाले रैखिक समीकरण युग्म
अध्याय 4 द्विघात समीकरण
अध्याय 5 समांतर श्रेढ़ी
अध्याय 6 त्रिभुज
अध्याय 7 निर्देशांक ज्यामिति
अध्याय 8 त्रिकोणमिति का परिचय
अध्याय 9 त्रिकोणमिति के कुछ अनुप्रयोग
अध्याय 10 वृत्त
अध्याय 11 रचनाएँ
अध्याय 12 वृत्तों से संबंधित क्षेत्रफल
अध्याय 13 पृष्ठीय क्षेत्रफल और आयतन
अध्याय 14 सांख्यिकी
अध्याय 15 प्रायिकता



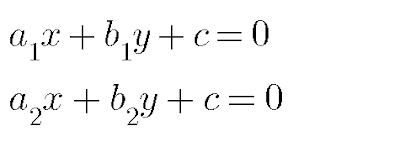


![सांख्यिकी {Statistics} [Chapter 14, Class IX]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi_Eie0g-2Q4WFhuq33fcbGc6APTAUgrqjls1icjZOeRuojnetcOlKLR-xFI9kWja-9vZYS968WIH5_w0nlOXC0SN8JiNSQfShnqHpcRjoLAOJ9QcIc48SIXNzPEhiCYgJJGs5dz_smlY0j/s72-c/Statistics+Class+9+CBSE.jpg)

7x+6y=3800
जवाब देंहटाएं3x+5x=1750