त्रिभुज की परिभाषा और प्रकार (Definition and types of Triangles)

त्रिभुज किसे कहते हैं? (परिभाषा)

तीन भुजाओं से बनी एक बन्द आकृति को त्रिभुज कहते हैं। त्रिभुज में 3 भुजाएँ, 3 कोण और 3 ही शीर्ष होते हैं। त्रिभुज सबसे कम भुजाओं से बनने वाली एक बन्द आकृति (बहुभुज) है। त्रिभुज के तीनों आन्तरिक कोणों का योग 180° होता है।

त्रिभुज के प्रकार

भुजाओं के आधार पर त्रिभुज 3 प्रकार के होते हैं। त्रिभुज का परिमाप हमेशा उसकी तीनों भुजाओं का योग होता है। त्रिभुज का क्षेत्रफल ज्ञात करने के लिए सबसे उपयुक्त सूत्र है:
1/2 × आधार × ऊँचाई

त्रिभुजों की परिभाषा और सूत्र नीचे दिए गए हैं:-

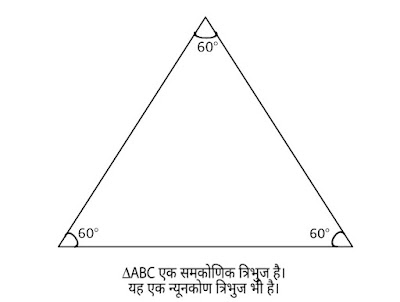
समबाहु त्रिभुज (Equilateral triangle):  जिस त्रिभुज की तीनों भुजाएँ बराबर हों, उसे समबाहु त्रिभुज कहते हैं। इसका प्रत्येक कोण 60° का होता है।

परिमाप = 3 × भुजा




समद्विबाहु त्रिभुज (Isosceles triangle):  जिस त्रिभुज की दो भुजाएँ बराबर हों, उसे समद्विबाहु त्रिभुज कहते हैं। इसकी बराबर भुजाओं के सामने वाले दोनों कोण बराबर होते हैं।

परिमाप = 2A + B
(सूत्र में A त्रिभुज की बराबर भुजाओं की माप और B तीसरी भुजा है।)
क्षेत्रफल = 1/2 × आधार × ऊँचाई

विषमबाहु त्रिभुज (Scalene triangle):  जिस त्रिभुज की तीनों भुजाएँ अलग-अलग लंबाई की हों, उसे विषमबाहु त्रिभुज कहते हैं। इसके तीनों कोण अलग-अलग होते हैं।

∆ABC
परिमाप = AB + BC + AC
क्षेत्रफल = 1/2 × आधार × ऊँचाई

● यदि त्रिभुज की तीनों भुजाएँ दी गई हैं और उपरोक्त किसी सूत्र की मदद से क्षेत्रफल निकालना संभव नहीं लग रहा, तो हीरोन के सूत्र से किसी भी प्रकार के त्रिभुज का क्षेत्रफल ज्ञात किया जा सकता है:

कोण के आधार पर भी त्रिभुज 3 प्रकार के होते हैं।

न्यूनकोण त्रिभुज (Acute angle):  जिस त्रिभुज का प्रत्येक आंतरिक कोण 90° से कम होता हैं, उसे न्यूनकोण त्रिभुज कहते हैं।

समकोण त्रिभुज (Right angle triangle):  जिस त्रिभुज का कोई एक आंतरिक कोण 90° (समकोण) होता है, उसे समकोण त्रिभुज कहते हैं।

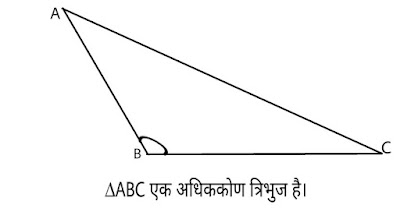
अधिककोण त्रिभुज (Obtuse triangle):  जिस त्रिभुज का कोई एक आंतरिक कोण 90° से अधिक होता है, उसे अधिककोण त्रिभुज कहते हैं।